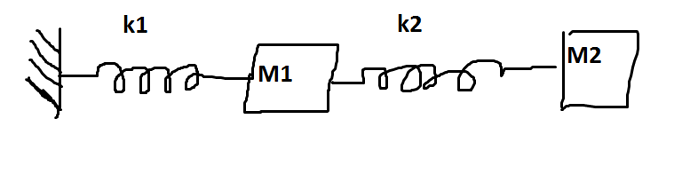
I'm trying to program a physical model for a spring - mass - spring - mass system.
It looks like this:
No friction and no gravity for now, only horizontal components of acceleration, referring to hooke's law.
This is the current object i'm working on
chaotic osc.axo (2.9 KB)
There are several knobs: time allows to edit the timefactor for the simulation (you should set this to something different than 0 if you want to use the object)
x0 sets the initial displacement for M2 mass.
k, h represent the elastic constants for the two springs
m1, m2 represent the two masses
when the reset inlet is triggered the system restarts the simulation from the x0 position.
The core of the code is this:
A1=(param_h*DX2-param_k*DX1)*281474976710656/M1; //calculating the acceleration in function of the displacement of the spring
A2=-param_h*DX2*281474976710656/M2;
V1+=___SMMUL(A1,param_time); //calculating the resulting speed (i'm doing a quite dumb integration here)
V2+=___SMMUL(A2,param_time);
X1+=___SMMUL(V1,param_time); //calculating the resulting displacement of the mass (i'm doing another dumb integration here)
X2+=___SMMUL(V2,param_time);
DX1=X1-LA<<4; //calculating the displacement of the spring relative to the rest position
DX2=X2-X1-LB<<4;Now, the system is well defined with these equations, there are only some tweaks to be done (i know this because i previously implemented the object with float operations and it worked well, set aside the enormous cpu load).
However, i need to tweak the parameters (and bitshift here and there), but i don't even know where to start.
I already tried some configurations, but they did result in unexpected behaviour (kinda like extremely fast fluctuatioons or absurd dynamic range or bizarre overflowing and acceleration going from +64 to -64 in just 1 cycle.
Can someone help me figure this out?