Polyphonic morphable wavetable oscillator

[thetechnobear]

PI think the antialiasing technique @johannes mentioned doesn't involve multiple waveform versions, but does require pre-processing of the waves, and extra code to decide them when playing them back.

do you have a link for this?
... the only method I found was FFT->strip harmonics -> IFFT, repeat for different frequencies. this could be preprocessed, but then you are required to store the resulting waveforms from the IFFT... you wouldn't need that many i guess. but the FFTs are needed to be with large number of bins to retain any resemblance to the original source.

[toneburst]

I think I may have been confusing a discussion here with one on another forum.

Try:
http://www.idmt.fraunhofer.de/content/dam/idmt/en/documents/Personal%20Websites/Franck/publications/dafx2012_hoiws_talk.pdf

There are other links, but about to go out. Will look them up later.

a|x

[toneburst]

The technique is known as DPW, I think (couldn't remember the name, earlier).

There's probably example sourcecode available.

The maths is way over my head, sadly.

a|x

[toneburst]

Here's the discussion I confused with one here, from the Mutable Instruments forum (look for pichettes posts):

http://mutable-instruments.net/forum/discussion/7163/sinc-interpolation/p1

Links to this paper:
http://dafx.ca/proceedings/papers/p_169.pdf

a|x

[thetechnobear]

interesting...
I did some digging, and think I understand the basic concept of DPW, but unfortunately, I think the 'meat' of how to integrate the 'generic' wavetables is detailed in a paper called "Higher-Order Integrated Wavetable and Sampling Synthesis" , so I think id have to buy that, as I can't find any details/implementations.
the only implementations/examples of dpw I could find were using specific waveforms... so they 'know' the integration function..
the p169 paper seems to just give examples, not how to do it, over and above 'integrate the wavetable'

frankly though, the maths is probably beyond me, without some working examples, so unlikely I will pursue this, unless I stumble on some more details somewhere.

besides, for my current purposes, my wavetables were fine when used in 'reasonable pitch ranges' and using a bit of LP filtering where necessary.

[thetechnobear]

ok, so kept digging and found this...
http://forum.cockos.com/showthread.php?p=1715341

desc:test PIWT
/* T.Rochebois 08/2016
  based on code developped at IEF/AXIS lab around 1997.
*/
slider1:32<4,512,1>Table length
// wavetable params
slider3:1<0,10>-R0
slider5:1<0,10>-R1
slider6:5.3<0,10>-I1
slider8:2<0,10>-R2
slider9:0.4<0,10>-I2
slider23:10<0.2,10>Glide rate
// ___________________________________________________________________
@init
function PIWT_init(nMax) instance(n x y z w dp _dp _dp3) (
  this.nMax = nMax;
  n = nMax;
  x = ad; ad += n;
  y = ad; ad += n;
  z = ad; ad += n;
  w = ad; ad += n;
  dp = n*440/srate;
  _dp = 1 / dp; 
  _dp3 = _dp * _dp * _dp;
);
// _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 
function PIWT_dcRemove(t n) local(i m)(
  m = 0;  i = 0; loop(n, m += t[i]; i += 1; );
  m /= n; i = 0; loop(n, t[i] -= m; i += 1; );
);
// _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _   
function PIWT_integ()
  instance(x n y z w z y x)
  local(i)(
  PIWT_dcRemove(x, n);
  i = 0; loop(n-1, y[i+1] = y[i] + x[i];                i += 1;  );
  PIWT_dcRemove(y, n);
  i = 0; loop(n-1, z[i+1] = z[i] + y[i] + (1/2) * x[i]; i += 1;  );
  PIWT_dcRemove(z, n);
  i = 0; loop(n,
    y[i] *= 1/2;
    x[i] *= 1/6;
    i < n-1 ? w[i+1] = w[i] + z[i] + y[i] + x[i];
    i += 1;
  );
  PIWT_dcRemove(w, n);
);
// _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 
// Call before aProc if there is a discontinuity of dp _dp
function PIWT_disc() 
  instance(n dp _dp _dp3 p out w z y x w0 w1 w2) local(p0 a)(
  p -= 2*dp; p += n * (p < 0); p -= n * (p >= n); p0 = p|0; a = p - p0; 
  w0 = w[p0] + a * (z[p0] + a * (y[p0] + a * x[p0]));
  p += dp; p -= n*(p>=n); p0 = p|0; a = p-p0;
  w1 = w[p0] + a * (z[p0] + a * (y[p0] + a * x[p0]));
  p += dp; p -= n*(p>=n); p0 = p|0; a = p-p0;
  w2 = w[p0] + a * (z[p0] + a * (y[p0] + a * x[p0]));
);
// _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 
function PIWT_aProc()
  instance(n dp _dp _dp3 p out w z y x w0 w1 w2 w3) local(p0 a)(
  p += dp; p -= n*(p>=n); p0 = p|0; a = p-p0;
  w3 = w[p0] + a * (z[p0] + a * (y[p0] + a * x[p0]));
  out = (w3 - w0 + 3 * (w1 - w2)) * _dp3;
  w0 = w1; w1 = w2; w2 = w3;
  out;
);
// ___________________________________________________________________
// Init the wave table
_srate = 1 / srate;
piwt.PIWT_init(512);
  dpLfo = 2*$pi*5.5*32/srate;
// ___________________________________________________________________
@slider
slider20 != aslider20 ? (
  dpc = (piwt.n*440/srate)*2^((slider20-69)*(1/12));
  abs(slider20 - aslider20) >= 12 ?  piwt.PIWT_disc();
  aslider20 = slider20;
);
slider1 !== aslider1 || slider3 != aslider3 
 || slider5 != aslider5 || slider6 != aslider6
 || slider8 != aslider8 || slider9 != aslider9 ? (
  slider1 = min(512,max(4,slider1|=0));
  piwt.n = n = slider1;
  piwt.dp =dpg = dpc = (piwt.n*440/srate)*2^((note-69)*(1/12));
  i = 0; loop(n,
    phi = 2*$pi*i/n;
    piwt.x[i] = sin(slider3 * phi 
      + slider6 * sin(slider5 * phi
        + slider9 * sin(slider8 * phi))); // <--- Rich wavetable
    i+=1;
  );
  piwt.PIWT_integ();
  piwt.PIWT_disc();
  aslider1 = slider1;  aslider3 = slider3;
  aslider5 = slider5;  aslider6 = slider6;
  aslider8 = slider8;  aslider9 = slider9;
);
// ___________________________________________________________________
@block
while (midirecv(offset, msg1, msg23)) (
  msg2 = msg23 & 0x7F; msg3 = msg23 >> 8; status = msg1 & $xF0;
  status == $x80 ? ( status = $x90; msg3 = 0; );  // note off
  status == $x90 ? (                              // note on
    msg3 == 0 ? (msg2 == note ? gate = gate2 = 0; )
  : ( 
      note = msg2;
      dpc = (piwt.n*440*_srate) * 2 ^ ((note - 69) * (1/12));
      gate2 == 0 ? (dpg = dpc;);
      gate2 = msg3 * (1/127);
      gate = sqrt(gate2);   
    );
  );
  midisend(offset, msg1, msg23);
);
// ___________________________________________________________________
@sample
k <= 0 ? (
  k = 32;
  pLfo += dpLfo; pLfo -= 2*$pi*(pLfo>0);
  dpg  += 32*_srate*slider23 * (dpc - dpg);
  piwt.dp = dpg * (1+ 0.01*sin(pLfo));
  piwt._dp = 1 / piwt.dp;
  piwt._dp3 = piwt._dp * piwt._dp * piwt._dp;
  piwt.PIWT_disc();
);
k -= 1;
env += (gate>env ? 0.01: 0.0001) * (gate - env);
spl0 = spl1 = min(2,max(-2,env*piwt.PIWT_aProc()));

I'll take a look at this, see if I can understand whats going on

[SmashedTransistors]

Hello,

Eh, that's one of my JSFX plugin

That's a 3rd order differentiation of a pre integrated wavetable:

• The @slider section calculates a wavetable (based on some kind of phase modulation but anything is possible here as long as it generates a wavetable)
• The function PIWT_integ does the pre integration step :
  • The function is considered as a set of polynomial segments (not isolated samples)
  • The pre integration consist in calculating the polynomial coefficients for the 3rd order integrated function.
  • x y z and w are tables that contain the polynomial coefficients for the third order integration.
• PIWT_aProc is the main function
  • p is the phase
  • dp is the phase increment
  • p0 is the integer part of the phase: aka the segment number
  • a is the float part of the phase
  • w3 is the more recent value of the 3rd order integral ( w3 = w[p0] + a * (z[p0] + a * (y[p0] + a * x[p0])); )
  • w2 w1 w0 are past value of the integral
  • out = (w3 - w0 + 3 * (w1 - w2)) * _dp3; is a third order differentiator with normalisation by 1 / dp^3

The problem with third order DPW is that it needs double precision.

I tried to summarize some ideas (including anti alias of distortions) in a small doc here :
http://stash.reaper.fm/28384/DifferentiatedPolynomialWaveTables.pdf

Maybe it is possible to do some 3rd order DPW by using some 64bit fixed point arithmetic...
but I'm still quite new to the Axoloti and a little clumsy with fixed point.

[Sputnki]

Is really that important to use third order integration? Couldn't you just stop to second order?

As for operation with 64bits, i fear it's not possible, not with floating point or fixed point, that's because of the architecture of the cortex M4. (Actually you can use 64bit floats, but they will make the cpu fly up into the sky)

What if you work with a decimated wavetable? (8bit)
I mean, if you need more precision i guess it's always relative to something else. If you aim to produce a 8-bit wavetable, having a 32-bit workspace should be plenty.

[SmashedTransistors]

Well,
with third order integration, as far as i experimented with JSFX/Reaper, at 48kHz there is almost no audible aliasing.

I think i will start with first order (I think that Johannes already implemented some first order DPW to generate bandlimited square). And give second order a try.

My goal is to implement a wavetable osc that can be phase modulated.
=> DPW with audio rate divisions.

I don't think that using a 8 bit table will be helpful.

The accuracy problems are both at the numerator and denominator sides.
The numerator is a difference of two polynomials.
The denominator is a difference of two consecutive modulated phases.

I think that the length of the table has a greater impact on the artefacts.
Maybe, some consistency tricks between the error in the numerator and denominator can help...
Well, I'll have to experiment somewhat.

[toneburst]

I'm watching this thread with interest.

Could you envisage the Axoloti being able to record samples and convert them to the band-limited wavetables you mention? It wouldn't necessarily have to do the pre-processing in realtime, but the ability to record a snippet of audio, then automatically create a wavetable from it would be great!

From my point of view, that's the killer feature most hardware wavetable synths lack (except for the Waldorf NW1 Eurorack module).

a|x

[jaffasplaffa]

the ability to record a snippet of audio, then automatically create a wavetable from it would be great!

@toneburst
You can do this with my wavetable patch, from the community library. Instead of using the sine/saw career subpatch you could use an input. I all ready experimented a bit with making wavetables out of all kinds of samples, internally in Axoloti. Works pretty well. In some cases it is favourable to add a window function to remove click, especially from movies clips, etc.

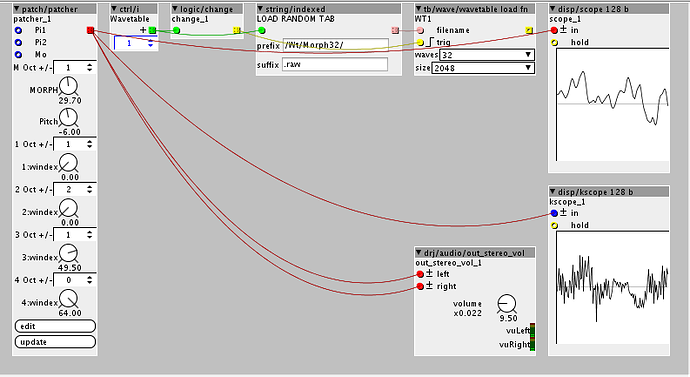
I also made a wavetable subpatch, which can morph between several waves. Here you go:
4 morph FOR COM 1.axp (27.7 KB)

You can use this version with a "multi wavetable", with more than 1 wave. Using @thetechnobear wavetable object it is pretty easy to set up.

If you for example have a 128 waves wavetable you can, with the index knobs, select 4 waves to morph between, with MORPH knob. And there is also an octave switch for each wave for extra fun

You can also make a wavetable consisting of only 4 waves and moprh between them. This is very "Sd-ram friendly", you get a lot of different waves and only use very little sd ram.

Id love if someone made a dedicated object like this, that were more efficient. And maybe with more waves to morph between.

[thetechnobear]

the ability to record a snippet of audio, then automatically create a wavetable from it would be great!

if you going down to single cycles, isn't this pretty much granular synthesis?
if your doing longer 'phrases' then this is slicing?

or are you thinking of something else?

my wavetable object could be relatively easily adapted to live input, it just using a table ... and it needs to know the table side (same for recording into a buffer, so no difference there) and number of waves... this currently is done at compile time (for efficiency /compiler optimisation), but make a 'variable' version, slightly less efficient is a tiny code change.

I think personally the issue, when you get into recording , is how does the user control this, and see whats going on... if you look at something like the push2 or octatrack they display the waves and allow the users to navigate thru it.... and I think you really need this to be useful.
squashing this all into the current scope type control is ok, as for now, but really we need more control than this.. e.g. bigger displays and more importantly it needs to be completely disconnected from the PC/Mac java UI to support the standalone nature of axoloti.
What I want to do, is have viewable display buffers, so that things like axocontrol and push2 could have this kind of 'interactive nature', and the user to be able to patch the interaction - but more on this at a later date

[jaffasplaffa]

if you going down to single cycles, isn't this pretty much granular synthesis?

if you for example use 128X 2048 waves = 262144 samples.. Which is around 5 seconds. Then you can make a wavetable out of a word or something like that. This sound a bit different than granular synthesis. Both are fun, though

[thetechnobear]

well, I guess sample playback, granular synthesis and wavetables are all related, basically chunking up waves and moving the origin point (some granular synths are pretty flexible with grain sizes )

anyway, Id wonder how you'd get reasonable cross points for record audio, its not like its going to 'magically' zero cross (or ends match directions) , so its going to be pretty crunchy.
I kind of thing of wavetables as being 'prepared' such that the individual waves are 'nicely formed', and even arranged in a manner, such that morphing makes sense.

hmmm... gives me an idea, this could be done with recorded data, if you did a bit of analysis ... a bit like is done with slicing. might be a slight delay, before the wavetable would be 'ready', as it would have to be done off the audio thread, to ensure no audio glitches.

[jaffasplaffa]

well, I guess sample playback, granular synthesis and wavetables are all related

Yeah related, but not the same. Wavetables are tuned, som they work the same way as an oscillator, you can play it like any oscillator, with the tonal benefits of an oscillator. Most granular stuff is a bit more diffuse. Maybe some granular effects you can sync the grainsizes to clock, but that is not the same as using it as a tunable oscillator. That is one of the main differences between wavetables and granular.

anyway, Id wonder how you'd get reasonable cross points for record audio, its not like its going to 'magically' zero cross (or ends match directions) , so its going to be pretty crunchy.

Not that hard to do. Use a window function when recording, so you get the fade in and out. As mentioned above, this is really important when trying to use for example audio from a movie, which has got complicated audio signal. In that case it can be hard to find a zero crossing, epsecially one that fits into the grid of the wavetable indexing.... So you have to make them yourself. I would suggest a custom window function for this, where you can control the fade in /out. The ones from fac.lib. have too much fade in/out for wavetable, IMO. If I remember correct, this is also how Serum does it.

End match; what do you mean by that? Length? If length, check my wavetable creator patch. It sets the length of how long of a wavetable you like to record. By default it is set to 262144 samples.

hmmm... gives me an idea, this could be done with recorded data, if you did a bit of analysis ... a bit like is done with slicing.

Yes, it can, check my patch in com lib. I have all ready made a recording wavetable thingy. But didnt work on it for a long time. Its all about doing calcuation before hand You use the oscillator tuned to fit in a table, using my example for 262144 wavetable(128X2048), the waves have to be 2048 samples long. The only way I got to do that was making a subpatch for it... Took a bit of timeto get it tuned... Actually I think i spend a WHOLE freakign weekend getting that right!!!!!

You can find that in my wavetable creator patch. It is called "Math tune" or something like that. It can be used to tune an oscillator to fir PERFECTLY into a table. Check with scopes, that the waveform doesnt move...Again this took LONG time go get right.... When this is set up, you add the windows function, which has to be controlled by the "table tuned" osc, so it makes fade in/out for each wave in the wavetable.

[geecen]

I was looking at the Oscitron Eurorack module by Soulby synths today - you can do the wavetable record thing on it. I think it synchs the wave recording to crossing through zero so they are always complete cycles. Don't know coding (yet! :)) but the code is available onlinee, so someone might want to have a look at how it's been done.

[SirSickSik]

I've been updating my wavetables in a different way since last week.
instead of reading out the waves from the wavetable module directly, I first "record" the wave from the external wavetable into an internal array of the same length as a single waveform in the wavetable.
During this recording a lowpass-filtering is applied realtime, re-writing the internal buffer constantly, adjusting the cutoff to the pitch being played (the higher the pitch, the lower the cutoff), turning it into a sinewave. This re-recording itself, recording this filtered signal, is also behaving like a filter, only applying the new, filtered, shape partly each loop (minimising differences which might cause unwanted overtones).
So when playing higher and higher notes, the internal wavetable that is read out by the phase of the oscillator will gradually turn into a sinewave, which can be played at any frequency up to nyquist/2 without creating unwanted frequencies.

[ivofx]

I found this free wavetable-editor, it's multi-platform (i.e. runs on Linux) and allows to export to wav-format.
https://synthtech.com/waveedit/
It does allow to import any audio-file and create wavetable slices. It's really fun to use on it's own.

[lokki]

yes, look here:

https://waveeditonline.com/index-1.html

you can download those wavetables and use them with the recent wavetable objects by @SmashedTransistors, really nice stuff.

[Jens_Groh]

See also here.