PDM-domain processing

#1

I've developed an experiment with oversampling:
Searching a way to downsample efficiently (with anti-alias filtering), lead to exploring the potential benefits of a high (32x) oversampling ratio at the compromise of only 1 bit per sample resolution. This is called "PDM" - pulse density modulation, the regular digital audio format is "PCM" - Pulse Code Modulation. The term "DSD" is also used but that's a trademark name.
All sorts of square waves can be expressed nicely. Regular square waves, but also multi-PWM waves can be made by combining multiple square waves with bitwise AND and XOR functions.
At 32x oversampling and one bit per sample, a group of 32 samples (corresponding to one regular PCM sample) fits in a 32 bit integer. The 32 bits now represent time domain, the value is "meaningless". Bitwise operations like AND and XOR can just operate on 32 samples in a single instruction... A bitwise ADD can be implemented, by expanding like a logic binary (full) adder circuit can be decomposed into primitive gates.

I made a test patch containing a PDM square wave oscillator, bitwise AND/XOR, and a PDM-to-PCM converter.
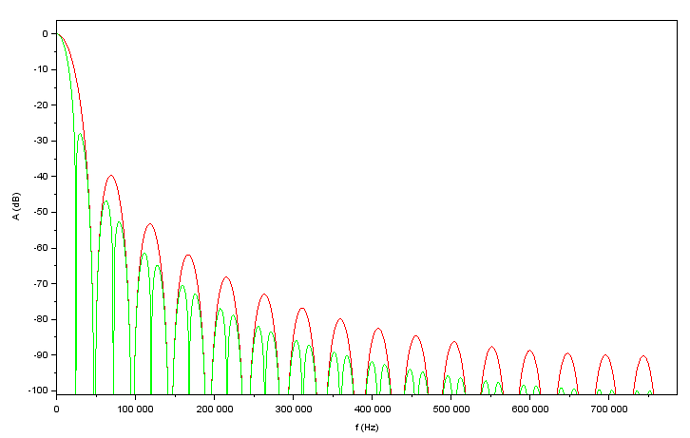
The PDM-to-PCM converter uses a 3th order CIC (Cascaded-integrator-comb) filter.

The test patch is in contrib/patches/jt/devel/pdm_workbench.axp

Ideas about further applications are invited: special square oscillator shapes? Other PDM-domain generators or processing algorithms?

some references:
https://en.wikipedia.org/wiki/Pulse-density_modulation
https://www.eecs.qmul.ac.uk/~josh/documents/ReissSandler-DAFX2004.pdf
http://www.emmlabs.com/pdf/papers/DerkSigmaDelta.pdf
http://sjeng.org/ftp/SACD.pdf

CIC filter response in red, the green plot is an additional null I added at Nyquist (after downsampling).

Pasted image726x461 5.16 KB

Upsampling / downsampling: am i doing it good?
#2

This looks cool!
Did your research into more conventional oversampling yield any interesting results?

@Jan came up with a novel method of using two outlets to carry two halves of a 32-sample buffer for 2x oversampling, combined with a downsampling object to combine them back into a standard 48kHz signal. Maybe there could be some kind of 'official' way of doing this. Perhaps a new inlet/outlet type for 2x oversampled signals?

a|x

#3

That sounds better and looks better also:
oldway

new way

#4

@toneburst Haven't dug into generic oversampling, I was specifically attracted by the 1-bit idea leading to very efficient processing. Adding general oversampled inlet/outlet types will need deep thoughts, if it's a separate datatype, the use of color to indicate a datatype is no longer a valid approach, since there 'd be x2, x4, x8, x16, x32 etc PCM datatypes, and perhaps x16, x32 and x64 PDM datatypes... The rainbow is too small... And what to do with interconnects between different rates? Making up/downsampling/filtering transparent (at interconnect) would require to build the filters into the framework, while there are many choices and trade-offs to be made when designing up/downsampling/filtering, they're not very generic.

@philoop the ripples that you observe in the old way are there on purpose, and serve to make the square wave bandwidth limited / alias free. https://en.wikipedia.org/wiki/Gibbs_phenomenon
The new way does not have it, it has a significant high-frequency attenuation compared to the factory square wave and pwm oscillator. The PDM-to-PCM converter could be improved with a "CIC compensation filter" to compensate the rolloff, and then it will have a similar ripple.

#5

Silly question here: is it possible to do distortions with this?

#6

While I haven't worked it out, I do think so, but the first missing element is a PCM-to-PDM convertor.

#7

It's kind of like converting the audio stream to a PWM signal...

a|x

#8

How can I find the patch, I did a git fetch on the Axoloti repository which as far as I know did the same for axoloti-factory and axoloti-contriib, but I still couldn't find axoloti-contrib/patches/jt/devel/ . I must be doing something really stupid here.

Not that this is really related to the topic, but there are microphones which output a PDM signal, such as the InvenSense ICS-43432. The ADAU1961 codec used in the Axoloti Core can interface directly which such a microphone using the JACKDET/MICIN pin. But it's not really relevant to this topic, as the codec always outputs PCM anyway.

#9

It's in the 1.0.10 branch of axoloti-contrib.

Besides PDM-domain processing, I think there is a more efficient square oscillator coming based on the CIC filter, but skipping the full PDM domain and reducing the cpu load further.

#10

Can PDM be used to approximate other types of waveform?

If it's possible to convert any arbitrary PCB stream to PDM, I assume it's also possible to create basic waveforms directly as PDM. I wouldn't know where to start attempting something that, though.

There's some information here about how the oscillators of the Roland Alpha Juno worked. Might be an interesting project to try and recreate them using PDM.

a|x

#11

Roland Alpha Juno pulse and sub-waves look very possible, just a matter of creating the PDM sequence. Unsure about the saw waves.

To make a sine wave PDM, you need a delta-sigma modulator. Not sure if it can be expressed efficiently.

General PDM wavetables could also be interesting, the per-sample workload to obtain 32 PDM-samples could probably just be extracting 32 PDM samples from the table from the right position, which corresponds to 32x oversampling, but there might be something completely wrong with this idea though - at DC there is only 5 bit of level info found in 32 bits.

#12

Added a PDM/CIC based squarewave oscillator test patch to
contrib/patches/jt/devel/cic_oscillator_workbench.axp
Internally it skips the PDM domain, as there are only 64 different 32bit PDM sequences involved, their corresponding CIC integrations can fit in a small lookup-table.

#13

That made me realize something, probably completely obvious, but here it goes: The information density (total bits/s) doesn't change between the PDM and PCM domains, with the configuration you describe. Then what seems to change is how the information is distributed in frequency space: in PDM you can represent very high-frequency signals. It then makes sense that the resolution at DC goes down.

#14

That being the case, I'm a bit confused how a generalised PCM to PDM converter would work, I have to admit. I can only visualise it as a particularly low-resolution PWM.

a|x

#15

I'm talking here about repetitions of the same 32 PDM samples, that occurs when reading out a PDM wavetable while the frequency is zero.
In non-repetetive PDM streams, the equivalent PCM DC component can sit in the ultrasonic content of the PDM stream, not limited to 5 bit.
https://en.wikipedia.org/wiki/Delta-sigma_modulation

#16

I really like these oscillators, I was wondering if they were going to be official at any point, any maybe having a few more flavors (PWM, triangle...)

#17

I'm confused, surely the PCM/PDM conversion process would be an implementation of the delta sigma algorithm?

#18

Hey @johannes

Really liking the square wave osc! Why did I miss that one :slight_smile: Any chance of development of a high quality saw osc ala the square osc?

Thanks :wink: