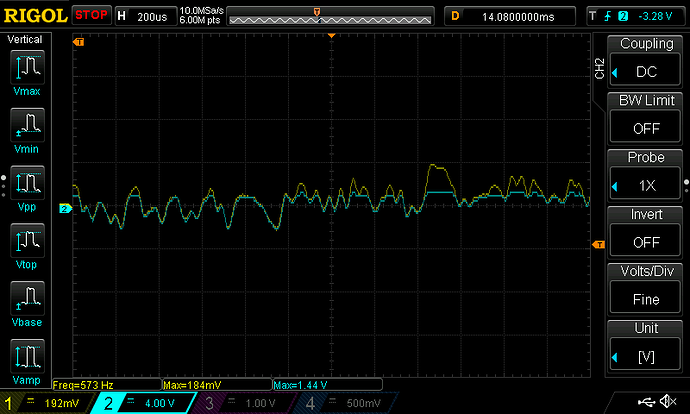
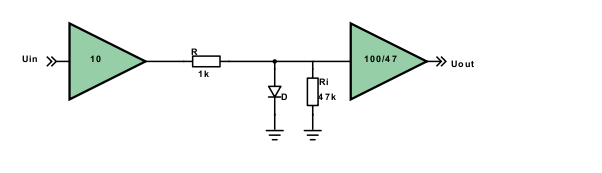
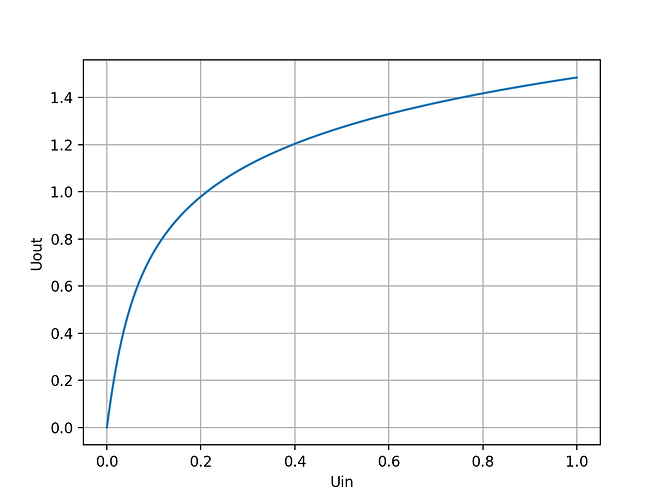
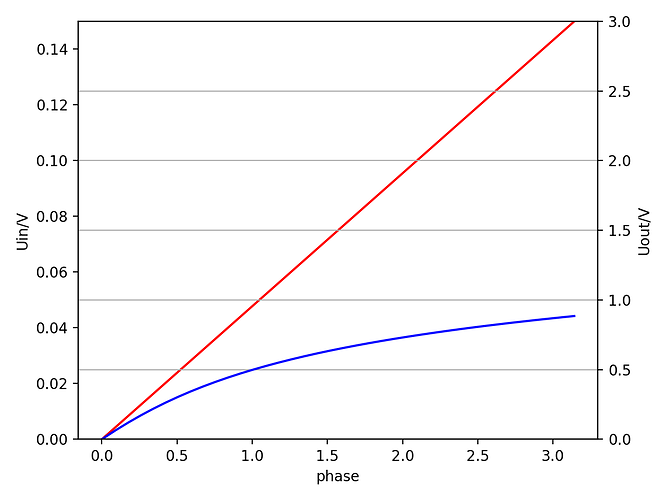
Hi everyone,
I'm about to start a journey into modelling analog circuits. The topic has been in my head for some time already and I want to finally get started. What I'm looking for now is some fellows to go through this together. In my experience ping-ponging ideas can greatly improve the experience for everyone and that's why I think it could be great to work on this together.
My goal...
... is to gain a deeper understanding about what matters in analog circuits and how to model some of the relevant behaviour in a DSP. Maybe we create some Axoloti objects for saturation/filters/vcas based on real circuits. But I consider the creation of new objects a side effect. Really, the primary goal, for me, is to learn and tinker.
My background
I'm currently approaching my final thesis in electrical engineering at a university in Germany. I have some background in DSP and signal theory as well as C/C++ programming. Add to that multiple years of experience building synths and synth modules (eurorack, it's a horrible drug). Why am I mentioning this? Because that says a lot about the angle from which I'll approach this topic.
Preferred methodology
To make this fun and interesting for everyone, I'd suggest we try to make things reproducible for everyone. That means we should be clear about what we did and how so we can all follow each others discoveries. Most importantly, I think we should stick to the same circuit until we all decide we want try something else.
My plan...
... is to start simple and slowly move forward. Ideally, I'd like to pick a circuit and build it. Then we can start making a model in the form of an Axoloti object/patch. With the right tools (oscilloscope, ears, circuit simulator, math, ...) we can compare the real thing to our model and slowly work towards a perfect model. If we succeed in one circuit we can pick the next, more complicated one. All of this will require patience and realistic goals.
Here's my roadmap, but this is more of a suggestion than a fixed schedule:
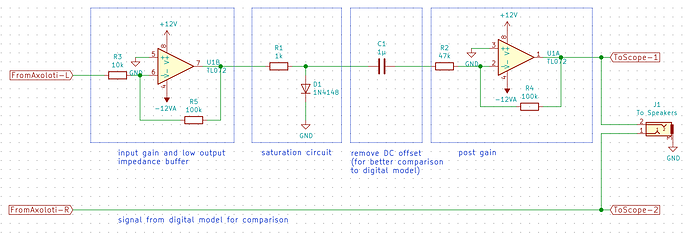
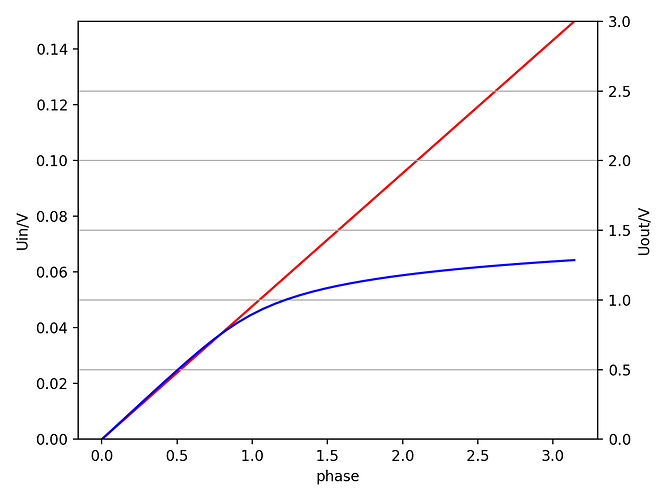
- Start with a simple circuit that involves only a minimal number of components, no feedback and preferrably only a single type of semiconductor. (My idea would be a simple diode saturation, but I'm open to anything)
- Decide on a realization of this circuit and build a test rig that we can use to measure stuff about this circuit.
- Create a specific object/patch to create test signals like certain oscillator shapes, impulses, sweeps, etc. We could use the community library or another github repo for this. That way, we all work with the same test signals and know that we're talking about the same thing.
- Setup an Axoloti patch to feed the test signals to both our real circuit and our model. If we use the left audio output to feed our (real) test circuit, we can use the right output for our digital model. That way, we can directly compare the real thing with our model using all kinds of test equipment.
- Create a first naive model by using simple math and circuit analysis. No worries about optimization at this point.
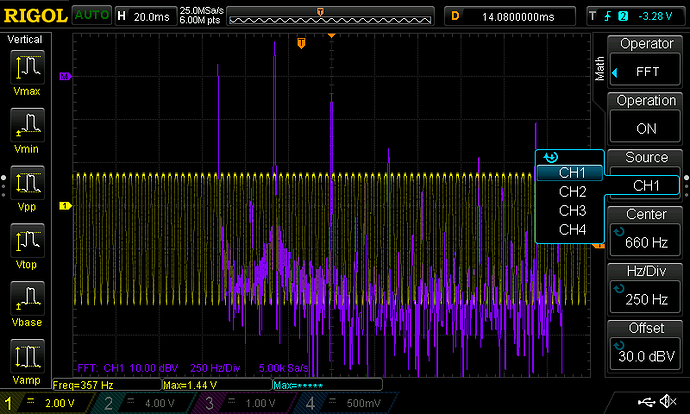
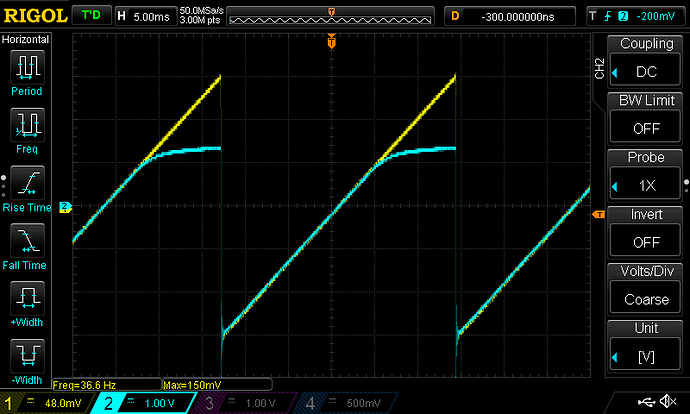
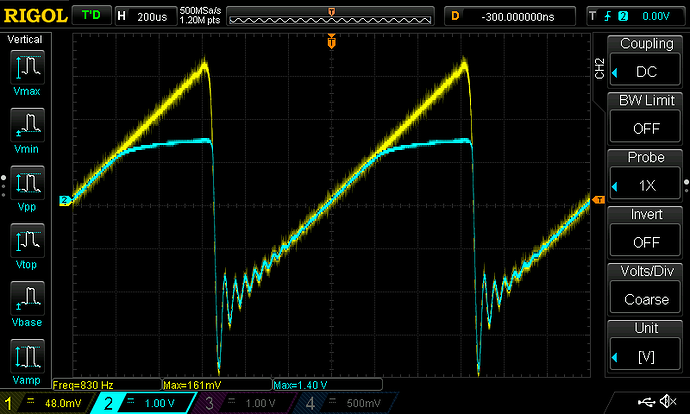
- From there on it'll be about comparing our model to the real thing by firing all kinds of test signals at it.
- If we succeed with our first simple model, I'd suggest we pick the next. I have some ideas about circuits to try.
My worries
All of this may sound like a rigid plan, but to be honest, I'm not even sure if this is the right approach. What do you think? I'm open for any suggestions, so please: Go ahead and let me know what you think about this.
Does all of that sound interesting to you? Let's go!