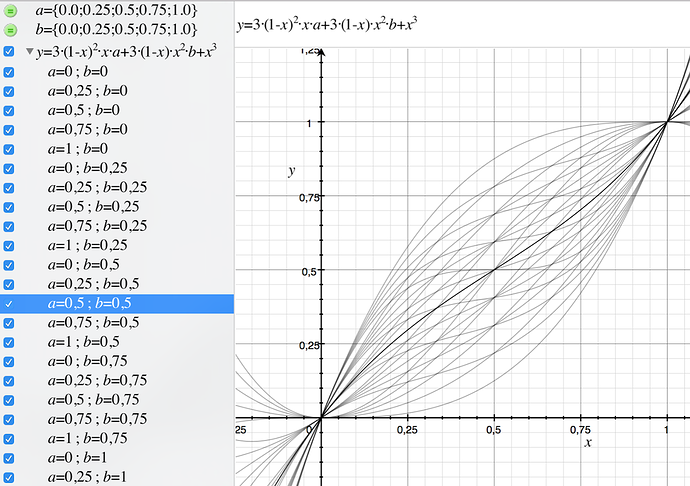
Fastest way to convert to/from int32 and float in 0-1 range

#41

Ok, 1D bezier, that looks suitable - and is also the solution to two parameters controlling the derivative at origin and endpoint (1;1) :slight_smile:

Pasted image1377x971 421 KB

#42

Poyfect!

Different solution to the same problem.

I don't know much about maths, and have no formal background in computer-science, but I used to do quite a lot of work in realtime graphics and video (using Quartz Composer, which is why I keep mentioning it), and I worked on a JavaScript Cubic Bezier implementation for a commercial client, a few years ago.

It's nice to be able to make a suggestion that proves useful, even when much of the discussion goes over my head, to my shame.

a|x

#43

Without the pow()s:

y=3*((1-x)*(1-x))*x*a+3*(1-x)*(x*x)*b+(x*x*x)

The only downside is it's not 100% intuitive what the a and b values actually do.

If this is reasonably efficient, it looks to be a good way for create a wide variety of interpolation curves.

Great work!

Time for bed...

a|x

#44

Does this convert int32_t to float 0 > 1 and back?
Is it faster than the first method you suggested?

a|x

#45

a is the slope at x=0
b is the slope at x=1

if you look at my grapher screenshot, you see all the 25 plots bundle at the origin into 5 bundles, each is one setting of a. Similar bundles shape up at x=1, they're different settings of b.

May I suggest to try "env/d lin" rather than "env/d" to feed into the 1dbezier? A regular "env/d" already has an exponential decay curve...

#46

Yes and yes. The speedup is very tiny compared to things like replacing pow(x,4) with (x*x)*(x*x).

#47

Yep, I realise that.

I meant it might be hard to explain to 'the average user'. I'm a technical adviser at a university here in the UK, and I've often struggled to explain bezier curves in drawing and DTP packages. My usual line is "it's harder to explain than it is to do". That only holds when you can see what's going on, though. It's a bit less obvious when you can't.

Grapher is great, by the way! I've not used it much before, but I'm learning how useful it is, now

a|x

#48

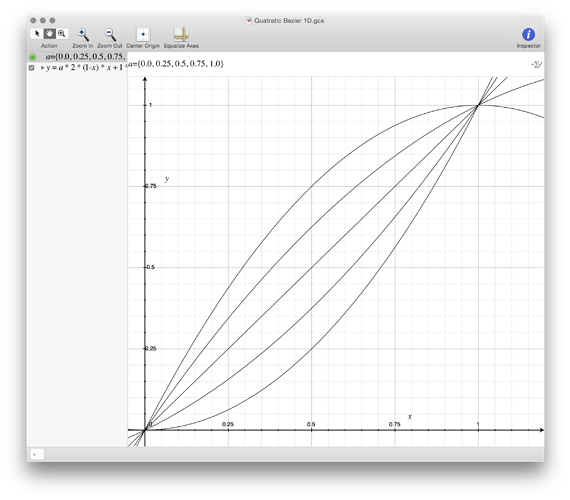
Here's the 1D Quadratic Bezier (from the same source), by the way.

y=a*2*(1-x)*x+(x*x)

Screen Shot 2016-05-13 at 09.33.31.png2400x2102 411 KB

Makes a nice straight line at a=0.5, unlike the Cubic Bezier, but it's a bit subtle for my porpoises, I think.

a|x

#49

Ah, I didn't realise that...
Will try that when I get home (have the Axo software here, but not the Axoloti Core hardware).

a|x

#50

@johannes Would you recommend I use your more recent int <> float conversion functions, or the earlier version you posted in my object?

I'm a bit unclear if your test code is intended to end up in the Axoloti Maths library, to be called from custom objects, or if you envisage it being used as-is in individual objects.

Also, should I be prefixing functions I create in the Local Data section of my object's XML code with the compiler instruction

attribute ((always_inline)) _STATICINLINE

a|x

#51

Will end up there in the next release, but don't rely on this in 1.0.10 patches and objects, as that will fail to compile.
Prefix with
__attribute__ ( ( always_inline ) ) __STATIC_INLINE
(your post doesn't show the correct underscores, I guess due to forum markup)

#52

Ah, OK. I'll make my own functions to do the conversion, then. I can just edit that by substituting a call to your functions later.

Just to be clear re. prefixing my object functions:
You recommend doing that in every case?

If you have time, could you briefly explain what the compiler instructions do? I have a feeling it's to do with no re-defining the same function more than once, but I may be wrong..

a|x

#53

That's odd...
I tried copying the float<>int conversion functions from your floats_workbench.axp into my object, and the number of cycles reported jumped from 4 before, using

float int2f(int32_t val) {
	return val * (float)(1.0f / (1 << 27));
}

int32_t f2int(float val) {
	return (int)(val * (float)(1 << 27));
}

to 27, using

__attribute__ ( ( always_inline ) ) __STATIC_INLINE float Q27ToF(int32_t op1) {
  float fop1 = *(float*)(&op1);
  __ASM volatile ("VCVT.F32.S32 %0, %0, 27" : "+w" (fop1) );
  return(fop1);
}

__attribute__ ( ( always_inline ) ) __STATIC_INLINE int32_t FToQ27(float fop1) {
  __ASM volatile ("VCVT.S32.F32 %0, %0, 27" : "+w" (fop1) );
  int32_t r = *(int32_t*)(&fop1);
  return(r);
}

..which was a bit of a surprise.

I think I'll stick with method 1. Unless the number of cycles is being misreported.

a|x

#54

There was some discussion about this earlier in this thread, I have now added
asm volatile("mov r0, r0");
barriers to patch/cyclecounter (sync libraries)
That should fix cyclecounter inconsistencies.

#55

I see.

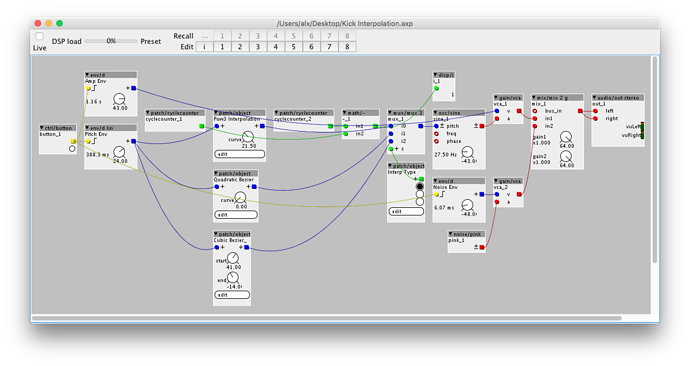
I've made interpolation objects for:

  • Pow4
  • Quadratic Bezier
  • Cubic Bezier

Screen Shot 2016-05-13 at 21.16.11.png1276x678 80.3 KB

@thetechnobear I did these for my own entertainment. Don't want to step on your toes, if you wanted to publish something similar (but probably better) to the Contrib library.

a|x

Kick Interpolations.axp (10.8 KB)

#56

Cool. Tbh im more interested in the cycling behavior , so these could be complementary for what I have in mind :slight_smile:

#57

Cool. I will publish them, then.

a|x