Sputnki contributions

#61

sptnk/math/rot 2d
sptnk/math/rot 2d k
sptnk/math/rot 3d
sptnk/math/rot 3d k

Geometric rotations for 2d and 3d coordinates.. Useful for lissajous applications.
Based on this: https://en.wikipedia.org/wiki/Rotation_matrix

sptnk/math/knee
sptnk/math/knee 2
Some k-rate mappings. You can see the meaning of parameters in the pictures. m stands for angular coefficient (in y = mx + q)

k.png834x364 4.96 KB

sptnk/math/grid
sptnk/math/grid k
Not sure if they should go in the math folder... Again, they're for lissajous purposes. These objects will generate a set of coordinates (with pitch) to form a grid with R rows and N columns.
Available in k-rate and s-rate

#62

Pitch detection objects:

sptnk/detect/0x k.axo
sptnk/detect/0x s.axo

These are very naive zero crossing detection objects, the former working at k-rate and the latter at s-rate.
These objects count how many samples occur between consequent zero crossings. The number of samples (green outlet) refers to the corresponding rate: k counts samples at k-rate and s count samples at s-rate.
No interpolation of any kind is implemented in these objects. The k-rate objects outputs a trigger pulse when a zero crossing has occurred.

sptnk/detect/0x k f.axo
sptnk/detect/0x s f.axo
Again, zero crossing detection in s-rate and k-rate. These however are slightly more precise, as they work in floating point and interpolate the wave in zero crossings. A conversion between sample period and frequency is also implemented (it's the frequency of a saw wave that goes from 0 to 64 in a number of samples equal to
the detected period

sptnk/detect/period mono.axo
This object is based on zero crossing detection, however it keeps track of the "mean value" and filters out readings that are too slow or too fast (maximum and minimum periods can be specified in the spinner boxes)
The objects starts to count when it finds a zero crossing in the signal.
While counting it checks if it encounters another zero crossing, and if the mean value of the signal is sufficiently close to zero (how close is specified by the tolerance knob) it outputs the readout.
Output is in number of samples (integer)
sptnk/detect/period mono f.axo
A variation on the previous object. This one interpolates the wave during zero crossings to achieve a better readout, and also outputs a frequency.

sptnk/conv/ftom.axs
This one converts a frequency to a midi note. You can see it as the "inverse" function of mtof. I tried to make it the most precise possible, however it still has a very little error, due to the non perfect logarithm computation. The error however is distributed as evenly as possible inside the whole -64 : 64 range

Feasibility of a spesific patch
#63

Distortion objects:

sptnk/effect fold 1.axo
Symmetrical waveshaper distortion based on 5th order polynomial, that folds the signal for sufficiently great values of the m parameter. Mildly antialiased, wild, with internal feedback and the ability to chain several waveshaper units with different m values.

sptnk/effect fold 2.axo
Symmetrical wavefolder distortion based on 5th order polynomial, looks like a sine shaper for intermediate values. Mildly antialiased, very very very wild, with internal feedback and the ability to chain several waveshaper units with different m values.

sptnk/effect waveshaper 16p.axo
Symmetrical waveshaper with user definable shape, similar to waveshaping with a table, but with "some sort of antialiasing that works well if you like it" added. This object has internal feedback and allows to chain several units together for utter sound devastation
Also
sptnk/effect waveshaper 16p coefs.axo
Allows to generate coefficients for the previous object.

You can see all the objects in action in the help file

#64

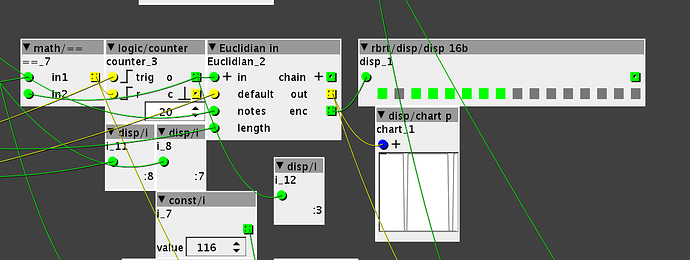
Hello Sputnki! i'm totally n00b but gettin my head around things and having a very good time :slight_smile: i'm struggling with euclidean objects. i had in mind to recreate the simple behaviour of Mutable Instruments Grids in euclidean mode, which is fairly simple (and has no offset or rotate parameter). it has a clock in and then you have three channels, on each one you can control length and fill (same as length and notes on yours). at first i had problems understanding that i needed a counter for your objects to work, now i kinda grasped it but still i don't know if i misunderstand them or if they behave in a way that i think is not how i understand euclidean pattern generators:
1) if you change the length parameter you also have to change the MAX count on the counter, otherwise if you have (say) length=8 and max count=16 you end up with only half of the pattern working. i managed to put a range dial controlled by midi cc that contemporarily controls MAX and length to have them always the same value. then another range dial for notes. it kinda works but i noticed that after a certain amount the actual filled steps start to decrease. then i realized it probably has something to do with the clock resolution i'm feeding it. i usually put up a midi clock receive object and then divide it by 6 to get a tick for each 1/16th. but , and here maybe i'm totally off, i think that for this to work correctly one will have to change the clock resolution WITH the max count AND the length, otherwise it doesn't work as i suppose it to. other problem i have to implement it for live purposes is that if notes > length it stops working, i'd have to find a way to constrain notes maximum range to length...but still bashing my head on the wall to find a solution :slight_smile: obviously the goal here is to have a realtime performance euclidean drum machine. thanks for any guidance in advance :slight_smile: i attach a zip with my patches if anyone wanna give it a check ! https://www.dropbox.com/s/qnh2dflp2vgmk4b/hyeuclid.zip?dl=0

#65

The basic principle of euclidean rhytms is to spread a number of notes and rests in the most uniform way possible.
The euclid.axo object i made (the one with notes and rests) takes notes and rests as parameters, so if you set it to work with 3 notes and 4 rests it will create a rhythm of 7 steps in total length, and it will spread notes and rests among these 7 steps.
Everything outside that range is treated as a rest (output is 0).
You can chain several objects together, to create complex rhythms, i.e. you could spread 2 notes and 3 rests over the first 5 steps and then 1 note and 2 rests over the next 3 steps.
If you want to wrap the rhythm over 8 steps you must do this before the first euclid object (use divremc)
Also, check the help patch in case you didn't!
P.s: euclid length.axo is really not much different, but instead of reasoning with notes and rests it deals with a total length and a number of notes. Rests are calculated as a difference between total length and notes

#66

sorry but still find it very confusing, i ask you a simple question:
with your implementation will i be able to just have one clock in , one knob to control length and one knob to control notes given just a maximum length, all realtime?
let's suppose i say the limit is 16 steps, will i be able to control realtime the two parameters, seamlessly changing both length and notes without issues? if it is possible i will do my best to understand it and implement it in my patch :slight_smile:
(by the way, ciao! :smiley: )

#67

Hi there,

can't compile any patch with granular player * series of objects,
always receiving errors like this

! C:\Users\Utente\DOCUME~1\axoloti/build/xpatch.h.gch
C:\Users\Utente\DOCUME~1\axoloti/build/xpatch.cpp: In member function 'void rootc::instancegranular__1::dsp(int32_t, int32_t, int32_t, int32_t, bool, int32_t (&)[16], int32_t (&)[16], int32_t&, int, int, int, int, int)':
C:\Users\Utente\DOCUME~1\axoloti/build/xpatch.cpp:248:160: error: 'class rootc::instancewrite__2' has no member named 'GAIN'
accum[j][grain_pan[i]]+=parent->instancewrite__2_i.array[USAT(grain_phase[i],27)>>(27-parent->instancewrite2_i.LENGTHPOW)]<instancewrite__2_i.GAIN>>param_gainreduction;
^
make: *** [C:\Users\Utente\DOCUME~1\axoloti/build/xpatch.bin] Error 1
shell task failed, exit value: 1
Compiling patch failed ( untitled )

#68

Hey, thanks for the report. Right now i can't check if there's any error in the code (i presume not), however i suggest you to check the name of the table the granular object points to (because the patcher it's signalling you that he can't find some variables that are normally present in table/alloc objects)
Maybe pm me or post here a screenshot of some stripped down version of your patch. Also check if there is an help object!)

#69

I feel that the problem is that I'm trying to assing a delay/write sdram table instead an alloc one :slight_smile:
I thought it was possible to find a workaround and make the granular player work with real time buffers

#70

Hi Sputniki! I'm using your Euclidian In object, and I'm wondering about something. I am using it to trigger an external synth, and I don't get a retrigger when two or more beats have a note. In other words, the pulse level stays high until there is a silent beat. Here is a screenshot of my patch:

Screen Shot 2017-12-03 at 9.11.01 PM.png1144x432 64.1 KB

Looking at the chart, you can see that the level stays high when subsequent beats have a note. In this example, I have length 8 and notes 7.
Is there any way you could tweek the code so the level would drop, or use a shorter pulse length? I took a peek at the code, but I am a novice and couldn't figure it out.
I would appreciate anything you could suggest. And thanks for all the contributions you make to the community!

#71

You could use a dirty hack: connect the counter output (green) with a logic/change and then logic/inv. This way you have a boolean signal that pulses every time the counter increments
You can then multiply this with the euclid object with logic/and, thus getting a trig output

#72

Cool, I'll try that. Thanks!
(edit) Yay! it worked!

#73

Hi Sputnki,

do you think there's a way to use the granular stereo player in real-time with live audio input?

#74

Unless you hack the object i'd say no way. Have you checked the factory grain delay?

#75

Hi Sputnki!

I think I found a bug on sptnk/math/cartesian2polar, both *k.axo and *s.axo. It outputted some unexpected values when I tested it. For example (10.00 ; 10.00) -> (5.51; 14.14) and (9.99; 10.00) -> (10.49; 14.14)

I think float param = 0.849; should be float param = 0.28125; instead. The website on the object description also uses this value to estimate arctan. (https://www.embedded.com/design/other/4216719/Performing-efficient-arctangent-approximation) What do you think?

BR, sellu

#76

Hi Sellu, thank you for the report. I will look into this bug when possible. In the mean time you could edit the object and correct it for your needs.
If i remember correctly, however, i adapted the formula in order to further reduce the error away from pi/4+ k*pi/2. It could be very well that the discontinuity stems from this personalization.

#77

re: your cartesian formula objects: so cool. after a few years of studying this stuff, I discovered these formulas and then came back here to ask if you'd have any interest in coding objects like this. quick search first and found that you did it three years ago, lol. thanks for all your work, this stuff is awesome.

#78

hey @Sputnkii reallly love your multi VCO object and have been using it as the main VA osc in my synth, but i just noticed some quite heavy aliasing noise on some frequencys of the sine wave. iirc i tested the factory sine at one point and it behaved similar, where as the MI sine doesn't do this. any idea on how to approach this?