Chaotic attractors

#1

Here is my first set of objects/patches to share. These are 2 chaotic attractors/oscillators.
The first one is the logistic map equation: x_(n+1)=rx_n(1-x_n),
logistic_osc.axo (778 Bytes)
logistic.axh (2.7 KB)
The first dial from the left labelled "r" is the value of r (in the equation above). Its range is between 3 and 4, mostly because for values of less than 3 the output is not interesting. (take a look here why: https://en.wikipedia.org/wiki/File:Logistic_Bifurcation_map_High_Resolution.png )
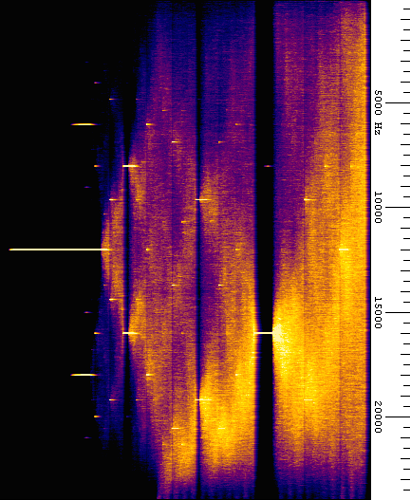
I run a spectrogram on the oscillator driven by an LFO so it would scan over all the (allowed) values of r and the output is this (x axis is r):

logistic_lin.png433x527 80.9 KB

The second oscillator is the Kawakami attractor
kawakami_osc.axo (856 Bytes)
kawakami.axh (2.1 KB)

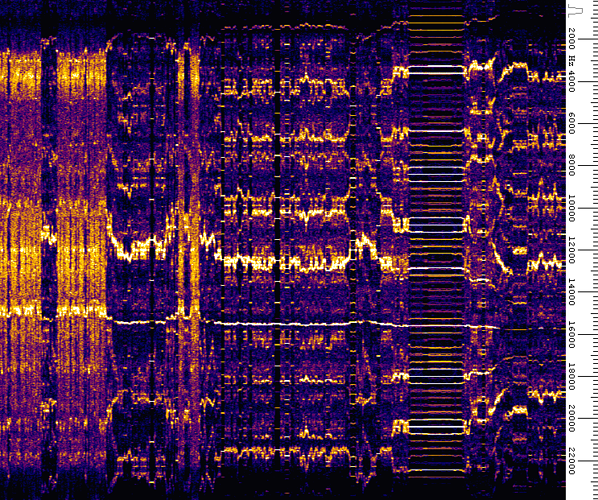
and here is the spectrogram, with time in the x axis at a fixed value (the default) showing how intermittent it is.

kawakami_lin.png743x621 248 KB

For some reason when changing the value of dial_2 (the only parameter for this oscillator) it sometimes goes into a cycle, so best to restart it. I think it has something to do with the initialisation of the x(n-1) and x(n-2) variables, but I haven't resolved this yet.
I thought that some might find these interesting as they are quite unusual in "normal" :smile: synthesizers.

#2

Whoa!
Those were quite harsh sounding even for me, wicked!
May i suggest a couple of things?
First of all: you should definitely sign into the contributors library, especially if (as i truly hope) you intend to do more of this stuff.
Second: I think you should add some way to tame this chaos, for example adding reset inlets (since very high or low pitches tend to phuck up the oscillations and make the oscillator unusable until patch restarts. See also if you can condition the logistic osc to a dial/b range without having to put stuff in front of it. Same thing for the output.
Third: maybe add more controls to the oscillators (if you have the knowledge try to add some audio rate sync input, that would make the oscillator übermäßig useful for "melodic" purposes)

As i have experienced, this community does not really care about math in a religious way, so you can make your personal interpretations of these oscillators without anyone being mad at you.

#3

Thanks for the feedback! :smile:
Yes I intend to do more of this. One of the ways to tame these oscillators is to make them generate the "next" value at a different frequency rate. I mean these are currently running at 48KHz but one can add a driver oscillator (e.g. a triangle) that triggers a latch and this generates the "next" value at the frequency of the triangle oscillator. That way one can tune them too. The problem is that I am struggling to create a sync-ed latch object running at s-rate.
About this locking of the oscillator, it is weird, I have to investigate a bit more why it happens. I implemented some of these in in SynC Modular (now long unmaintained) that did not have this behaviour.
Good idea to try to scale the oscillator to avoid the extra controls. Will look into this.
I have a few other oscillators in mind, so stay 'untuned' :wink:

#4

Right, I found a way to intialise the Kawakami oscillator each time the single parameter it has is changed at k-rate. However I am struggling to find how to generate a random number (uniform is fine) between 0 and 1.
I found that there is a GenerateRandomNumber() routine that I can call, but how do I scale this in the 0..1 range?
Many thanks for any help.

#5

Great work !

Tip for new lfo/osc - lorenz, rossler attractors and chua oscillator.

#7

I think the normalising factor for the output of the GenerateRandomNumber() function is 1<<27.

a|x

#8

Thanks for the tips! I have implemented the lorenz oscillator (not in the axoloti, in other softsynth). At some settings it sounds like an old engine (!) and it tends to go out of range quite easily. I'll try to build an axoloti version.

#9

Lorenz attractor oscillator.

10.7.2016 updated !

lorenz_osc.axh (1.4 KB)
lorenz_osc.axo (1.1 KB)

#10

Lorenz attractor clocked lfo.

lorenz_lfo.axh (2.4 KB)
lorenz_lfo.axo (1.2 KB)

#11

Chua chaotic oscillator.

chua_osc.axh (1.4 KB)
chua_osc.axo (1.2 KB)

#12

Nice. Can you add these objects to the community library as well? It's easier for everyone to use them, as they will be available in the Axoloti patcher.